Day 5: More Problems

We had our non-stop 4 hour math class today, and I accumulated lots of problems, so today's post is purely dedicated to problems:

1. Two charges q and -2q are kept a distance d apart. Assuming the origin at the 'q' charge and '-2q' at x=d, draw a graph of electric field intensity(E) versus position(x).

2. 9 lattice points ( 3 dimensional points whose x,y,z coordinates are all integers) are joined by 9C2=36 lines. Prove that at least one point exists on one of these lines which is an integer.

3. Solve sinx + cosx + |sinx-cosx| > √2

4. Draw the graph of 1/x+1/y=1/k, where k is a constant.

5. Find the angle at which the curve of sinx,cosx and tanx intersect the x-axis

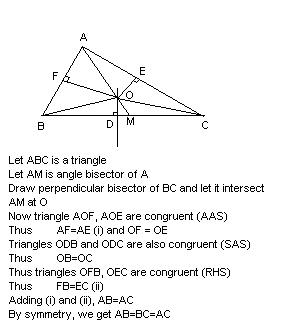
And if nobody gets the equilateral triangle proof anomaly, then I declare it tomorrow..

Today's Formula:

If x, y and z are three sides of a triangle, then |x|+|y|<|z|

"If you sit to study for 2 minutes, it seems like 2 hours, but if you sit with a nice girl for 2 hours, it seems like 2 minutes. This is the theory of relativity." -Albert Einstein

Day 4: Module IV

Today was more NES, more protests, more HC Verma electrostatics problems, and much more of Batch 1. We had our first class of module IV today, and our modules have grown much bigger, and much more comprehensive after the pattern change of JEE last year. The batch is a great mix of comedians, philosophers, time-passers and dominantly, geniuses.

We had our Physics-Mathematics today, and both teachers are excellent at explaining and entertaining, although the Physics teacher seems to overdo it a bit. But one thing has changed for the worse, and that is our Chemistry teacher.

Our last teacher, Mr. Purushottam, shared a great tempo with our batch. He is the best chemistry teacher at our centre. Ms. Monica, our new teacher, is difficult to adjust with (you can imagine our problems because she has to write 256 and 16 like class III children one below the other to add them). We demanded the authorities to change our teacher back to Mr. Purushottam, but they did not pay any heed. Then we decided to write a petition with signtures of about 15 students and fax it to Chennai (head office of Brilliant Tutorials). But I am apprehensive of their decision.

Back to the world of computers, check out this cool mp3 which recites digits of pi. Also download Celestia, with which you can explore the universe in a 3D simulation, and visit planets, stars, constellations, sattelites etc. A really addicting game called Pocket Tanks which is based on projectile weapons and tanks is available here.

Today I realized that LCM is defined not only for rational numbers, but also for irrational numbers. Here I quote the proof that (2)½ is an irrational number:

Let (2)½ be a rational number such that (2)½=p/q, where p is an integer, q is a natural number, and p/q is in its lowest form

or, p²=2q²
Thus p² is an even number, so p is also an even number
Let p=2k
thus, 4k²=2q²
or, q²=2p²
Thus q² is an even number, so q is also an even number
This contradicts the assumption that p/q is in lowest form, since the common factor 2 exists.
This completes the proof.

No questions today either, so you'll have to wait till tomorrow. Till then, ciao.

Today's Formula:

Lowest common multiple of two rational numbers p/q and P/Q is given by

LCM(p/q, P/Q)=LCM(p,P)/HCF(q,Q)

Day 3: Of Nintendo, Reservation Protests, Electrostatics, Knoppix and Batch 1

Whoa! The title itself is an antithesis.

First things first, I started Class XII (with respect to IITJEE) today with Electrostatics from HC Verma. The theory in this book is really amazing. I'll post some questions later..

On finishing the lullaby story describing the nuances of "a relativistic particle, having velocity comparable to velocity of light, may experience a change in mass, but never a change in charge", I booted the Knoppix LiveCD I recieved from INOI last year. I tried running Wine to play Windows games on Linux, but failed miserably with only 3 games running out of 10.

Today, our reshuffled batches list was announced (Oh, did I mention that I take coaching from Brilliant Tutorials). I reached the centre to see that I was assigned Batch 1, meaning I could study from all the cool teachers. 10 minutes later, I was answering frantic calls and SMS'es asking me about my friends' results. Finally, goodbye Manoj Khanna, goodbye Sanjay Tiwari....

When I got back home and switched on the television, I saw the mob of medical students take head on the brunt of police brutality. Water cannons, smoke grenades, teargas shells....., it seems Delhi Police has an unlimited arsenal for mob control. Buses full of arrested students left the site. The worst part is, that no political party, even the opposition, has taken any stance on this issue. This caste reservation scheme has gone too far, and Arjun Singh is surely going to have a Rang De Basanti-like showdown.

After all the hullabaloo, and the news channels having switched to Sansani, Murder, Vardaat etc. , I started playing on Nintendo (popularly known in India as "Video Game"). The nostalgia of playing all-time classics like Super Mario Bros, Contra, Tennis is simply exhilerating.

Due to availability of NES emulators, it is now possible to play these and many other games on your PC. Get FCEU, the NES emulator from here and game roms from here.

Today's Formula:

If there exist two point charges, q and Q, such that the distance between them is r, then the force of attraction/repulsion , F , between q and Q is given by

F=qQ/4πεr²

Day 2: Porsche Finally Unleashed

Need for Speed 5: Porsche Unleashed is one of the first realistic racing games in the NFS series. It features Porsche cars from the classic era to the modern era and has the usual singleplayer, multiplayer, knockout, tournament modes like the previous NFS titles. The hit point, however, is the realism and depth of this game, minus the flashy graphics, animations and effects of NFS Underground et al. Take a look at some screenshots


I finished the game today in 4 hours, and it was really enthralling. (4 hours of my pitiful, fruitless life down the drain, 4 hours closer to my pitiful, fruitless JEE).

And then I sat down for DC Pandey Subjective, did 2 questions in 15 minutes, got bored, and started geometry instead. Back to class VIII geometry.......

Try these for a change:

1. A line AB and a line CD intersect at O, and another line XY is drawn. Prove that there exist 2 points on XY which will be equidistant from AB and CD. When will there be only 1 such point?

2. In a quadrilateral ABCD, AC is the angle bisector of angle A as well as angle C. Prove that the diagonals are perpendicular to each other.

Oh yeah, if you havent seen this before, munch on this,

I can prove that all triangles are equilateral...



Please leave a comment if you can find the anomaly in this proof, and have not seen it before.


Todays formula:

If a, b, c are sides of a right triangle, c being the longest, then a²+b²=c²

Day 1: Hello World

void main()
{
cout<<"Hello World\n";
}

The customary Hello World, every programmer starts his journey with this peice of silly english. I mean, who would want to "hello" the "world".

Anyways, I started the first day of my last school summer holidays (oxymoronically speaking), with MCQ Maths, A Dasgupta. I planned to take on 2 questions from each topic of class XI. Easier said than done. Later in the day, I also did geometry for class VIII. (St. Lines etc. Believe me, they get really tough questions)

The most beautiful thing that I discovered today was the Pigeon Hole Principle (PHP). Click here to see what Wikipedia has to say about it. This is to number theory as quantum mechanics is to physics. As an example, I quote the following Friendship Theorem proved using PHP.

In a party of six or more people, at least three people exist who have met each other, or atleast three people exist who have never met each other.

Flabbergasted!?! This is a new genre of mathematics for me, and I'm gonna practice it tomorrow.


Today's formula:

cos(theta)+i*sin(theta)=e^(i*theta)